Wiskunde.netLogo Wiskunde


De Gulden Snede

LET OP: Wil je ook toegang tot meer dan 15.000 video-uitwerkingen voor 36 euro per jaar? Meld je dan snel aan! Klik hier...
Wiskunde01-12-2024admin23
De Gulden Snede

Inleiding

Het geheim van De Gulden Snede is een stukje, oude, raadselachtige Wiskunde. We komen De Gulden Snede op diverse plekken tegen. Zo vinden we deze terug in de architectuur, bij de lengte van je vingerkootjes, in de verhoudingen van je gezicht en zelfs bij groente, zoals bloemkool. De Gulden Snede duiden we aan met een getal. Dat getal noemen we φ (phi). Het getal φ (phi) geeft een verhouding weer. Men noemt dit ook wel de goddelijke verhouding (Divina Proportia).

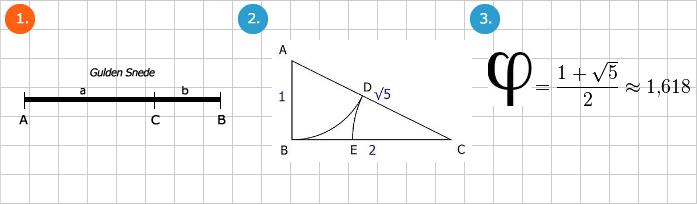
Wat is De Gulden Snede nu precies? Het probleem waar Euclides enorm mee stoeide, kunnen we het beste als volgt beschrijven. Stel we hebben een lijnstuk AB (afb.1). En we verdelen dit lijnstuk in 2 stukken door ergens een punt te kiezen. Hoe lang moeten de lijnstukken zijn zodat: de verhouding tussen het grootste lijnstuk AC en het kleinste lijnstuk BC gelijk is aan de verhouding tussen de hele lijn AB en het langste stuk AC? Meer wiskundig bekeken, levert dit: "Waar ligt C op AB zodat geldt: AC : BC = AB : AC.".

Stel dat BC = b en AC = a dan volgt verder: a/b = (a+b) / a. De verhouding a/b heet het gulden getal. Het gulden getal duiden we aan met φ. Als we nu a/b = φ invullen, dan levert dat: a/b = a/a + b/a => φ = 1 + 1/φ. Als we nu links en rechts vermenigvuldigen met φ krijgen we: φ2 = φ + 1 => φ2 - φ - 1 = 0. Dit is een kwadratische vergelijking en deze kunnen we oplossen met de abc-formule.

Hieruit volgt dat:

φ1 = (1+√5) / 2 = 1,618033988...

en

φ2 = (1-√5) / 2 = -0,618033988...
De laatste waarde is negatief. Vergeet deze maar even want aan een negatief lijnstuk hebben we niet veel. Dit getal φ houdt dus in dat lijnstuk AC 1,618.. keer zo groot is als lijnstuk BC en lijnstuk AB 1,618.. keer zo groot is als lijnstuk AC.

Formule De Gulden Snede

Waar ligt C op AB zodat geldt: AC : BC = AB : AC, met φ = (1+√5) / 2 ≈ 1,618

Voorbeelden De Gulden Snede

Constructie De Gulden Snede met passer en liniaal (afb.2)

Een mooie constructie van De Gulden Snede met passer en liniaal gaan we hieronder uiteenzetten:
- Teken een rechthoekige driehoek ABC, met AB=1 en BC=2. Via de Stelling van Pythagoras weten we dat AC=√5.
- Maak een cirkel met middelpunt A en straal AB en laat deze snijden met AC in punt D.
- Maak een cirkel met middelpunt C en straal CD en laat deze snijden met BC in punt E.
- Nu weet je; EC = DC = √5 - 1.
=> EC = √5-1
=> BE = 2 - EC = 2 - (√5-1)
=> BE = 3 - √5
Hieruit volgt => BE x BC = 6 - 2√5 = EC2 Dus: BE / EC = EC / BC, maw de zijde BC is verdeeld in De Gulden Snede.

Extra

De Gulden Snede heeft interessante eigenschappen:

- De Gulden Snede leidt tot gelijkvormige vlakverdeling.
- De Gulden Snede komt voor in vijfvoudige symmetrie
- De Gulden Snede is de verhouding van opeen volgende getallen in de Fibonacci reeks.
Hoe groter de getallen in de reeks, hoe meer ze De Gulden Snede benaderen.
- Naast het toepassen van De Gulden Snede op een lijnstuk, kunnen we deze ook benaderen als we een oppervlak of een cirkel opdelen in 2 stukken.
- Zoals vermeld is de waarde van φ = 1,61803398874989 enz. Pak je rekenmachine en neem eens het kwadraat van φ. Bekijk tevens wat 1/ φ oplevert. Wat zie je? De cijfers achter de komma blijven bij het kwadraat van φ en 1/φ steeds hetzelfde. Magisch!

Wiskunde.net © 2013 - 2024