Wiskunde.net

Symmetrie

01-06-2025admin23

Inleiding

Bij figuren die symmetrisch zijn, is er altijd sprake van een vorm van gelijkheid. De figuren bestaan dan uit gelijke delen. Er zijn vier vormen van symmetrie; spiegelsymmetrie, schuifsymmetrie, draaisymmetrie en puntsymmetrie. Het woord symmetrie komt uit de Griekse oudheid: ‘symmetros’. Dat betekent "gelijke maat houdend" of "passend bij".

Bij spiegelsymmetrie bestaat een figuur uit twee helften die we precies op elkaar kunnen leggen. Bedenk hierbij wel dat één van deze twee helften na omklappen ondersteboven op de ander komt te liggen. Een praktisch voorbeeld hiervan is een vlinder. We zeggen ook wel dat door vouwen je beide helften op elkaar kunt leggen. De vouwlijn is de spiegel-as of symmetrie-as. Je kunt ook de "helft" van een symmetrische figuur tegen een spiegel houden. Je ziet in de spiegel de symmetrische andere helft.

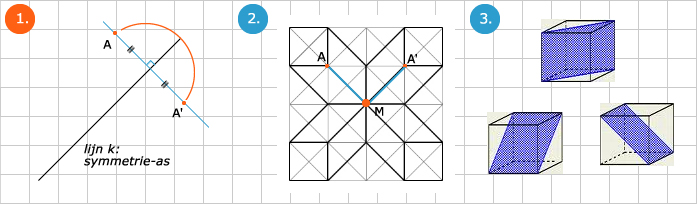
In een spiegel-as kun je ook een punt A spiegelen (zie afb.1). Je tekent dan door A de middelloodlijn op de spiegel-as en de afstand van A naar de spiegel-as is hetzelfde als de afstand van de spiegel-as naar A'. A' is dan dus het spiegelbeeld van A. Je kunt dit ook mooi met een passer doen. Een vierkant heeft vier spiegelassen, een rechthoek twee en een cirkel (mits de spiegel-as door het middelpunt gaat) oneindig veel spiegelassen.

Een figuur heet schuifsymmetrisch als hij een echt deel heeft, zodat: als je dat deel steeds verschuift over een vector of pijl, je de hele figuur krijgt. Zo zou je bijvoorbeeld een vierkant van 2x2 cm steeds 1 cm naar rechts en 1 cm omhoog kunnen schuiven. Het resultaat is een nieuwe figuur die schuifsymmetrisch is. Schuifsymmetrie kom je vaak tegen bij randversieringen.

Bij draaisymmetrie kunnen we de figuur (afb.2) als het ware optillen, een stukje draaien, en dan weer neerleggen zodat we weer de oorspronkelijke figuur zien. Het aantal keren waarmee we dit kunnen doen binnen 360 graden noemen we de orde. Zo kun je bijvoorbeeld een vierkant optillen, 90 graden draaien, weer neerleggen en dan heb je weer het oorspronkelijke vierkant. Dit kun je 4x doen binnen 360 graden. De orde is dus 4. Een figuur dat pas weer op zichzelf past als je hem 360 graden gedraaid hebt, is niet draaisymmetrisch (orde is 1). Het punt waarom je draait, noemen we het draaipunt. Een voorbeeld van draaisymmetrie is een reuzenrad.

Een figuur heet puntsymmetrisch als hij uit 2 helften bestaat die elkaars spiegelbeeld zijn in een punt. Dit punt heet het symmetriepunt. Symmetrie komen we ook tegen in de ruimte. We kunnen een ruimtelijke vorm in 2 stukken hakken. Als beide stukken dan precies gelijk zijn, is de snede het snij- of spiegelvlak. Ofwel symmetrievlak. Zo kun je een kubus op meerdere manieren in 2 gelijke stukken hakken. Een kubus heeft nl. 6 symmetrievlakken (zie afb.3).

Voorbeelden Symmetrie