Wiskunde.net

Driehoek van Pascal

01-06-2025admin23

Inleiding

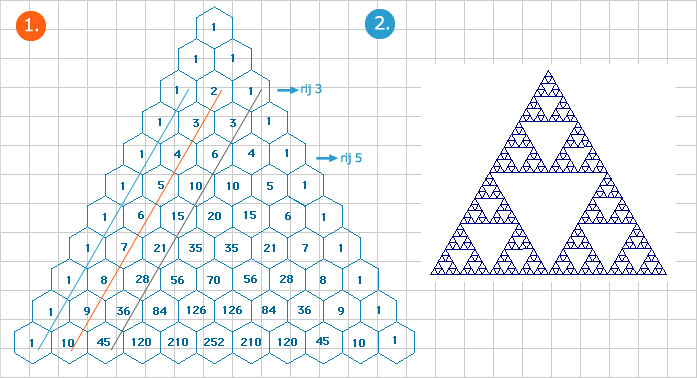
De driehoek van Pascal is een magische en dus een zeer bijzondere driehoek. Deze driehoek is niet een echte driehoek, maar een piramide van getallen. Je begint met het getal 1. Deze zet je in de 1e rij. Daaronder in de 2e rij zet je ook 2 enen. Op de 3e rij zet je de som van de getallen die erboven staan. Zo is bijvoorbeeld de 6 in de vijfde rij de som van 3 + 3. En is de 10 in de zesde rij de som van 4 + 6. Op deze manier kun je de piramide opbouwen. Aan de randen van de rij zet je steeds een 1. Dus de linker- en rechterdiagonaal bevat allemaal enen.

Magische eigenschappen van de driehoek:

1. De piramide (driehoek van Pascal) is symmetrisch in de verticale as. Deze loopt door de top recht naar beneden. De linker- en rechterkant zijn gelijk.
2. Bijzondere 11. De eerste rij is hetzelfde als 11 tot de macht 0, nl. 1. De tweede rij is gelijk aan 11 tot de macht 1, nl 11. De derde rij is gelijk aan 11 tot de macht 2, nl 121. De vierde rij is gelijk aan 11 tot de macht 3, nl 1331. De vijfde rij is gelijk aan 11 tot de macht 4, nl 14641.
3. De eerste linker diagonaal (blauw) bevat allemaal enen. De tweede linker diagonaal (oranje) is de rij 1, 2, 3, 4, 5, 6 t/m 10. Mooie rij, toch? De derde linker diagonaal (grijs) is de rij 1, 3, 6, 10, 15, 21, 28 enz. Dit zijn driehoeksgetallen. Bij driehoeksgetallen gaat het erom hoeveel bolletjes je nodig hebt om een gelijkzijdige driehoek grafisch weer te geven. Bijvoorbeeld 4 bolletjes op de grond, dan 3 bolletjes erboven, dan 2 erboven en dan nog 1 als topje. Samen 10. De volgende diagonaal 1, 4, 10, 20, 35, 56 enz. zijn de vierhoeksgetallen.
4. De som van de rijen is een macht van 2. De som van de 5e rij is 16. Dat is 2 tot de macht 4. De som van de 6e rij is 32. Dat is de vijfde macht van 2. Dus de som van rij n is 2 tot de macht (n-1). Dus de som van de 11e rij is 1024. Reken maar na!
5. Stel we nemen (1+x) x (1+x) x (1+x) = (1+x)³. We krijgen dan 1 + 3x + 3x² + x³ Je ziet dat de getallen voor de elementen, gelijk zijn aan de getallen in de overeenkomstige rij (n). In dit geval was n=3. Vul tevens voor x=1 in dan krijg je hetgeen we hebben laten zien bij punt 4.
6. Nullen en enen geven. Dit is 1 van de mooiste. Stel we vervangen alle oneven getallen in de driehoek door 1 en alle even getallen door 0. Je krijgt dan een bijzonder patroon. Deze komt overeen met de zeef van Sierpinski. Zie hiervoor afb.2.

Extra

Gerelateerd