Wiskunde.netLogo Wiskunde


De normale verdeling

LET OP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen voor 36 euro per jaar? Meld je dan snel aan! Klik hier...
Wiskunde01-06-2025admin23
De normale verdeling

Inleiding

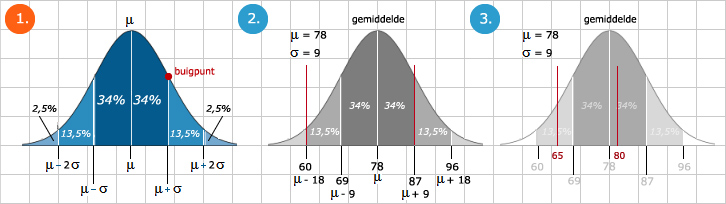
In de statistiek is de normale verdeling een erg belangrijk onderdeel. Bij een frequentieverdeling hoort een kromme die lijkt op een klok (klokvormig). Deze klokvormige kromme is symmetrisch waarbij het gemiddelde, de mediaan en de modus precies samenvallen. Het gemiddelde geven we weer met μ. We spreken dit uit als mu. Het gemiddelde ligt precies op de symmetrieas van de klokvormige kromme. De standaarddeviatie (σ) speelt hierbij ook een belangrijke rol. We hanteren een paar vuistregels bij de normale verdeling. Er wordt gesteld dat 68% van de waarnemingen ligt in het gebied tussen μ-σ en μ+σ. Daarnaast ligt 95% van de waarnemingen in het gebied μ-2σ en μ+2σ (afb. 1).

Stel dat de normale verdeling staat voor de lengte van de Nederlandse mannen. Waarom is deze normaal verdeeld? Dat komt omdat er links en rechts van het centrale midden (ongeveer) evenveel waarden liggen. Bij een kromme die gaat over de leeftijden waarop men luiers draagt, is het duidelijk dat deze kromme rechts-scheef is. Want een persoon zal alleen een luier dragen tussen het 0e en 4e levensjaar en er zijn maar weinig mensen die een luier dragen tussen hun 5e en 70e levensjaar. In afbeelding 2 zie je dus dat 68% van de mannen heeft een gewicht tussen de 69 kg en 87 kg. Je ziet ook dat 2,5% van de mannen zwaarder is dan 96 kg en dat 2,5% van de mannen lichter is dan 60 kg. Afsluitend stellen we dat 95% van de mannen een gewicht heeft tussen de 60 kg en 96 kg.

Formule De normale verdeling

Van de waarnemingen ligt 68% tussen μ-σ en μ+σ en 95% tussen μ-2σ en μ+2σ.

Voorbeelden De normale verdeling

Voorbeeld 1 (afb. 2)
Gegeven een groep mannen waarvan het gemiddelde gewicht μ = 78 kg. En de standaardafwijking σ = 9 kg.
Bereken hoeveel procent van de mannen weegt tussen de 60 kg en 87 kg.

Uitwerking:
De linkergrens is 60 kg en de rechtergrens is 87 kg. Daar horen de percentages bij: 13,5% + 34% + 34% = 81,5%.
Dit houdt dus in dat 81,5% van de mannen heeft een gewicht dat ligt tussen 60 kg en 87 kg.

Voorbeeld 2 (afb. 3)
Voorbeeld 1 geeft een duidelijke uitleg als de grenzen liggen op μ ± σ of μ ± 2σ. Maar hoe berekenen we het percentage van de mannen dat ligt tussen de 65 kg en 80 kg? We gebruiken hiervoor een optie op je GR (grafische rekenmachine).
We maken dan gebruik van de optie: normalcdf(l, r, μ, σ), met:
l = linkergrens
r = rechtergrens
μ = gemiddelde
σ = standaardafwijking

Uitwerking:
Antwoord = normalcdf(65, 80, 78, 9) ≈ 0,5136
Dit betekent bij deze normale verdeling dat de kans dat een man een gewicht heeft tussen de 65 kg en 80 kg gelijk is aan 0,5136. Of dat 51,36% van de mannen een gewicht heeft tussen 65 kg en 80 kg.
Online normalcdf berekenen

Extra

- De standaarddeviatie bij een normale verdeling is ook met het oog te schatten. De standaarddeviatie is namelijk het buigpunt van de normaal kromme (zie afb. 1). Dus bij dit buigpunt ga je recht naar beneden en lees de waarde af op de horizontale as (minus μ).
- Bij een verdeling met de top naar links, spreken we over een rechts-scheve verdeling. Voorbeeld: luiers dragen op welke leeftijd?
- Bij een verdeling met de top naar rechts, spreken we over een links-scheve verdeling. Voorbeeld: leeftijd waarop men grijze haren krijgt.

Gerelateerd

Standaarddeviatie De standaarddeviatie is een belangrijk begrip in de statistiek. De standaarddevi...
Procenten Wat zijn procenten? Bij procenten gaat het om een verhouding: deel / geheel. Ho...
Symmetrie Bij figuren die symmetrisch zijn, is er altijd sprake van een vorm van gelijkhei...

Video

Wiskunde.net © 2013 - 2025