Wiskunde.netLogo Wiskunde


Fibonacci

LET OP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen voor 36 euro per jaar? Meld je dan snel aan! Klik hier...
Wiskunde01-06-2025admin23
Fibonacci

Inleiding

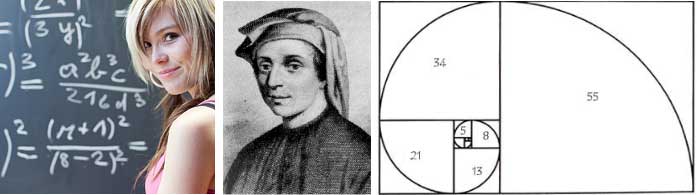
In de bekende film De Da Vinci Code van Dan Brown wordt Jacques Sauniere vermoord en achtergelaten. Op zijn lichaam worden 8 getallen als aanwijzing aangetroffen. Na bestudering van deze getallen (13, 3, 2, 21, 1, 1, 8 en 5) en door deze op volgorde te zetten, ontdekte men een bijzondere cijferreeks. De reeks 1, 1, 2, 3, 5, 8, 13, 21, 34, ... noemen we de Fibonacci-rij of Fibonacci-reeks. Deze getallen reeks is een van de beroemdste in de Wiskunde. De Fibonacci-rij is wereldberoemd vanwege de vele magische eigenschappen die kunnen worden ontdekt door met de rij te experimenteren.

De basiseigenschap is dat iedere term in de rij, de som is van de 2 termen er voor. Je begint met 1,1,.. dus de derde term is 1+1=2. Je krijgt dan 1,1,2,... De vierde term is dan 1+2=3. Je krijgt dan de rij 1,1,2,3,... De vijfde term is dan 2+3=5. Je krijgt dan de rij 1,1,2,3,5,... Met een computerprogramma kun je zo een oneindig lange rij laten genereren. De Fibonacci-rij wordt in de praktijk op vele plekken aangetroffen. In de natuur vinden we deze terug in het aantal windingen die door de pitjesspiralen van zonnebloemen worden gevormd. Ook in verhoudingen die architecten gebruiken om kamers in hotels te definieren, zijn bekend. Ook in de klassieke muziek vinden we vele oorsprongen van de Fibonacci-reeks.

Formule Fibonacci

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .. => n-de term = ∑ ( t(n-2) + t(n-1) )

Voorbeelden Fibonacci

Voorbeeld 1: De Fibonacci-som
De Fibonacci-reeks is dus te formuleren als 1,1,2,3,5,8,13,.. Maar wat gebeurt er als we daar de som onderzetten?

Fibonacci
De som van de eerste n termen van de rij van Fibonacci is telkens 1 minder dan de 2e term die op de n-de term van de rij volgt. Zo kunnen we dus snel zien dat de som van de eerste 9 termen is 89-1=88. Het antwoord van de som is dus altijd een ander Fibonacci-getal -1 (2 termen verder).

Voorbeeld 2: Kwadratische Fibonacci
We kunnen ook elk element uit de reeks met zichzelf vermenigvuldigen, dus het kwadraat nemen. En we maken tevens een nieuwe rij met de som van alle voorgaande kwadraten. Dan krijgen we onderstaand overzicht:

Fibonacci
Zie het getal 714. Dat is de som van alle vorige kwadraten. Dus 1+1+4+9+25+64+169+441=714. Maar 714 is ook 21x34. Magisch! Dus de som van alle kwadraten tot en met de n-de term is hetzelfde als het vermenigvuldigen van de n-de term uit de oorspronkelijke Fibonacci-rij met de volgende term. Zo is dus 1870=34x55.

Extra

De oorsprong van de Fibonacci-rij ligt in het konijnenpaar probleem. Fibonacci wilde weten hoe de voortplanting bij konijnen zou gaan op basis van een aantal aannamens. Hij wilde weten hoeveel konijnen er zouden zijn als een nieuw konijnenpaar na 1 maand zou werpen.

Gerelateerd

Driehoek van Pascal De driehoek van Pascal is een magische en dus een zeer bijzondere driehoek. Deze...
De Gulden Snede Het geheim van De Gulden Snede is een stukje, oude, raadselachtige Wiskunde. We ...
Wet van Benford Neem eens een aantal getallen. Veel getallen. Dat kunnen statische gegevens zij...
Stelling van fermat De Stelling van Pythagoras zegt dat a2 + b2 = c2, waarbij a, b en c de zijden v...

Wiskunde.net © 2013 - 2025