Wiskunde.net

Sinus

01-06-2025admin23

Inleiding

De sinus (en cosinus) zijn twee hele bekende begrippen bij goniometrische functies. Vanuit de oudheid zijn de sinus (en cosinus) de verhoudingen in een rechthoekige driehoek. Hierbij speelt de grootte van de driehoek geen rol; bij gelijkvormige driehoeken zijn de hoeken namelijk even groot. Het is hier wel van belang dat we spreken over een rechthoekige driehoek. Op basis van de SOS CAS TOA regels kunnen we hoeken en zijden berekenen. De sinus heeft de bekende golflijn.

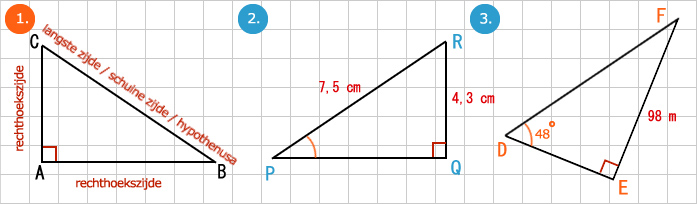
In afbeelding 1 zie je een rechthoekige driehoek. Deze bestaat uit een rechte hoek A (∠A) en 2 rechthoekszijden AB en AC. Een rechte hoek is 90 graden. Als we kijken naar hoek B (∠B) dan is AC de overstaande rechthoekszijde van ∠B en AB de aanliggende rechthoekszijde van ∠B. Zijde BC is de schuine zijde. Deze noemen we ook wel de hypothenusa. Met de formule sinus = overstaande rechthoekszijde / schuine zijde kunnen we de hoeken en zijden berekenen in een rechthoekige driehoek. De sinus is altijd een verhouding tussen 2 zijden. Met sin^-1 (een knop op je rekenmachine) bepalen we de hoek in graden.

Formule Sinus

Voorbeelden Sinus

Extra

Gerelateerd