Worteltrekken
 01-01-2026
01-01-2026 admin
admin 23
23
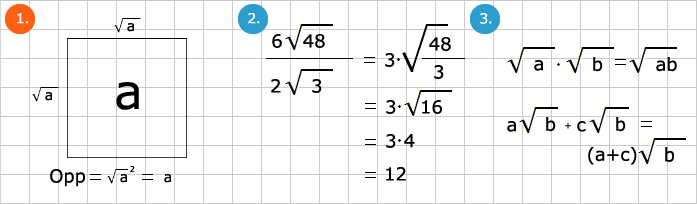
Inleiding
Worteltrekken is het omgekeerde van kwadrateren. Het kwadraat van vijf is 52 = 25. Het omgekeerde levert √25 = 5. Een wortel is de zijde van een vierkant met oppervlakte a. De lengte van de zijde is dan √a (afb.1). Het is handig als je de kwadraten van 1 t/m 15 uit je hoofd kent om zo makkelijk met wortels te kunnen rekenen.
Het nemen van de wortel uit een getal a komt neer op het zoeken naar een getal dat in het kwadraat a oplevert.
Dit is makkelijker als a een kwadratisch getal is. Deze operatie is zeer moeilijk als a geen kwadraat is van een geheel (natuurlijk) getal.
Rekenregels bij worteltrekken
1. (√a)2 = a
2. √a ⋅ √b = √(ab)
3. a√b + c√b = (a+c)√b
4. √(a/b) = √a / √b
Voorbeelden Worteltrekken
1) Kwadrateren van wortels (zie rekenregel1)
Wanneer je een wortel van natuurlijke getallen kwadrateert dan is de uitkomst altijd een natuurlijk getal.
(4⋅√3)2 = 4⋅√3⋅4⋅√3 = 16⋅√3⋅√3 = 16⋅3 = 48
2) Herleiden van wortels
Wortels moet je altijd proberen te herleiden (kleiner te schrijven). Dus om een zo klein mogelijk getal "onder" de wortel te krijgen.
Je gaat dan op zoek naar het grootste kwadraat waarmee je het getal onder de wortel kan vermenigvuldigen.
Voorbeeld 1:
√80 = ? Om √80 te herleiden, gaan we kijken door welk grootste kwadraat we deze kunnen delen. Het heeft geen zin om kwadraten te proberen die groter zijn dan de helft van 80.
Is √80 deelbaar door 36? Antwoord: nee.
Is √80 deelbaar door 25? Antwoord: nee.
Is √80 deelbaar door 16? Antwoord: ja.
Dus we schrijven √80 nu als volgt: √80 = √16⋅√5 = 4√5
Voorbeeld 2:
√192 = √(64⋅3) = √64⋅√3 = 8√3
3) Vermenigvuldigen van wortels (zie rekenregel2)
Bij het vermenigvuldigen van wortels vermenigvuldig je de getallen "voor" het wortelteken met elkaar en de getallen "onder" het wortelteken vermenigvuldig je met elkaar.
Dus a√b ⋅ c√d = ac√bd
Voorbeeld 1:
3√16 ⋅ 2√25 = 6√400 = 6⋅20 = 120
En dat klopt want je weet ook: 3⋅4⋅2⋅5 = 120
Voorbeeld 2:
4√7 ⋅ 6√11 = 24√77
4) Optellen en aftrekken van wortels (zie rekenregel3)
Je kunt alleen gelijksoortige wortels optellen en aftrekken. Gelijksoortige wortels zijn wortels die beide hetzelfde getal "onder" de wortel hebben.
Het getal "voor" de wortel doe je dan plus en/of min.
Voorbeeld 1:
3√7 - 2√7 + 6√7 = 7√7
Voorbeeld 2:
3√5 + 3√6 - √5 + 5√6 = 2√5 + 8√6 (kan niet kleiner)
Soms dien je (op het eerste gezicht niet-gelijksoortige) wortels te herleiden (vereenvoudigen) voordat je ze kan optellen.
√150 + √54 = 5√6 + 3√6 = 8√6
5) Breuken onder de wortels (zie rekenregel4)
Als er een vervelende breuk "onder" de wortel staat, dan dien je eerst de hele weg te werken. Daarna neem je de wortel van de teller en de wortel van de noemer.
Dus je werkt naar √(a/b) toe.
Voorbeeld 1:
√ (5 4/9) = √(49/9) = √49 / √9 = 7/3 = 2 1/3
Voorbeeld 2:
√ (7 3/4) = √(31/4) = √31 / √4 = √31 / 2 = ½√31
6) Wortels delen (zie rekenregel4)
Zoals je weet kun je gewone getallen delen door gewone getallen. Zo kun je ook alleen maar wortels door wortels delen. Als je een gewoon getal door een wortel wilt delen,
dan dien je dit gewone getal ook als een wortel te schrijven. Dus de wortel wordt dan van het kwadraat van dit getal.
Voorbeeld 1:
6√48 / 2√3 = 6/2 ⋅ √48/√3 = 3 ⋅ √(48/3) = 3 ⋅ √16 = 3 ⋅ 4 = 12 (afb.2)
Voorbeeld 2:
6 / √9 = √36 / √9 = √(36/9) = √4 = 2
Extra
Een lijstje van mooie wortels:
√1 = 1
√4 = 2
√9 = 3
√16 = 4
√25 = 5
√36 = 6
√49 = 7
√64 = 8
√81 = 9
√100 = 10
Gerelateerd
ABC Formule Hoe werkt de abc formule? De vergelijking ax²+bx+c=0 is de basisvorm van ee...
Oppervlakte trapezium Wat is een trapezium? Een trapezium is een vierhoek waarvan minstens 1 paar over...
Video's
Word ook lid!
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


