Wiskunde.net

Pi

01-12-2024admin23

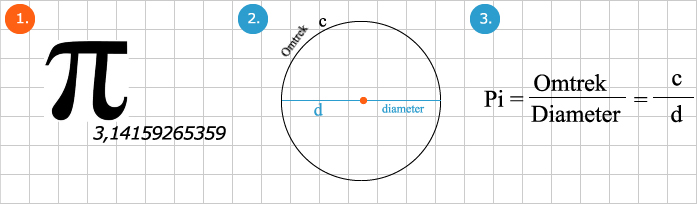
Inleiding

Het getal π = 3,14159... is een van de geheimzinnigste en interessantste getallen. Het heeft vanaf het begin een belangrijke rol in de wiskunde gespeeld en is ook tegenwoordig nog onderwerp van onderzoek. Het getal π komt in veel gebieden van de wiskunde voor: meetkunde, getallentheorie, analyse, kansberekening, enzovoorts. De definitie is eenvoudig: π is de verhouding tussen de omtrek en de diameter van een cirkel (afb.2). Met andere woorden: uit de diameter d volgt de omtrek C, wanneer we d met π vermenigvuldigen.

Reeds de Babyloniërs en de Egyptenaren wisten rond 2000 v.Chr. al dat de verhouding tussen omtrek en diameter bij alle cirkels gelijk is. De Babyloniërs rekenden met 3,125, de Egyptenaren met 3,16049. Ook in de Bijbel treffen we een bepaalde waarde van π aan. In het eerste boek Koningen wordt bij de bouw van een rond waterreservoir gezegd: 'En hij maakte het van de ene kant tot de andere tien el breed..., en een touw van dertig el was de omtrek. Hieruit volgt dat π = 3, een benaderingswaarde die ook volgens de toenmalige inzichten slecht was.

π is een irrationaal getal, het is geen breuk, het is een onmeetbaar, ja zelfs een transcendent getal. Dat betekent dat de getallen vanaf een bepaalde positie niet repeterend kunnen zijn.

De eerste die inzag dat π niet exact berekend, maar slechts systematisch benaderd kon worden, was Archimedes (287-212 v.Chr.). Zijn methode hield in dat hij in en rond een cirkel regelmatige zeshoeken tekende, waarvan hij de omtrek kon berekenen. Door het aantal hoeken steeds te verdubbelen was hij in staat om π steeds nauwkeuriger te berekenen. Bij 96-hoeken was het resultaat: 3 10/71 < π < 3 1/7.

Het huidige wereldrecord in de berekening van π staat op naam van de Japanner Yasumasa Kanada van de Universiteit van Tokio. ln septenber 1999 kwam hij in zijn berekening van π tot het ongelooflijke aantal van 206 miljard cijfers, een prestatie die overigens geen praktisch nut heeft. Het is net zoiets als de Mount Everest beklimmen zonder zuurstofmasker: niemand heeft er wat aan, maar het geeft een waanzinnig gevoel.

Formule Pi

Voorbeelden Pi

Extra

Gerelateerd